So, In these situations, often what you’re witnessing the frustration of a novice problem-solver, and power of an expert problem-solver.

It turns out theres a whole field of research on this.



Apologies for how dry this might about to get, but before I can really begin talking about how this research relates to play, I need to explain a little bit about what problem-solving research says, and it’s a bit nuanced.

Problem-Solving Research is an area of research which, in service of finding superior educational methodologies, attempted to discover the underpinnings of, you guessed it: problem-solving. This should make sense too, because having good problem-solving skills is sort of like having a magic bullet for learning.

Another way to think of good problem-solvers, is as strong self-learners.



The primary distinction between strong problem-solvers and weak problem-solvers, is their ability to solve what are called non-routine problems.



Routine, and Non-Routine are going to be pretty key terminology for the rest of this talk, so I want to make sure I’m clear on what they mean.

Routine problems are problems that the learner knows how to solve based on past experience. For example, finding the product of 567 and 46.



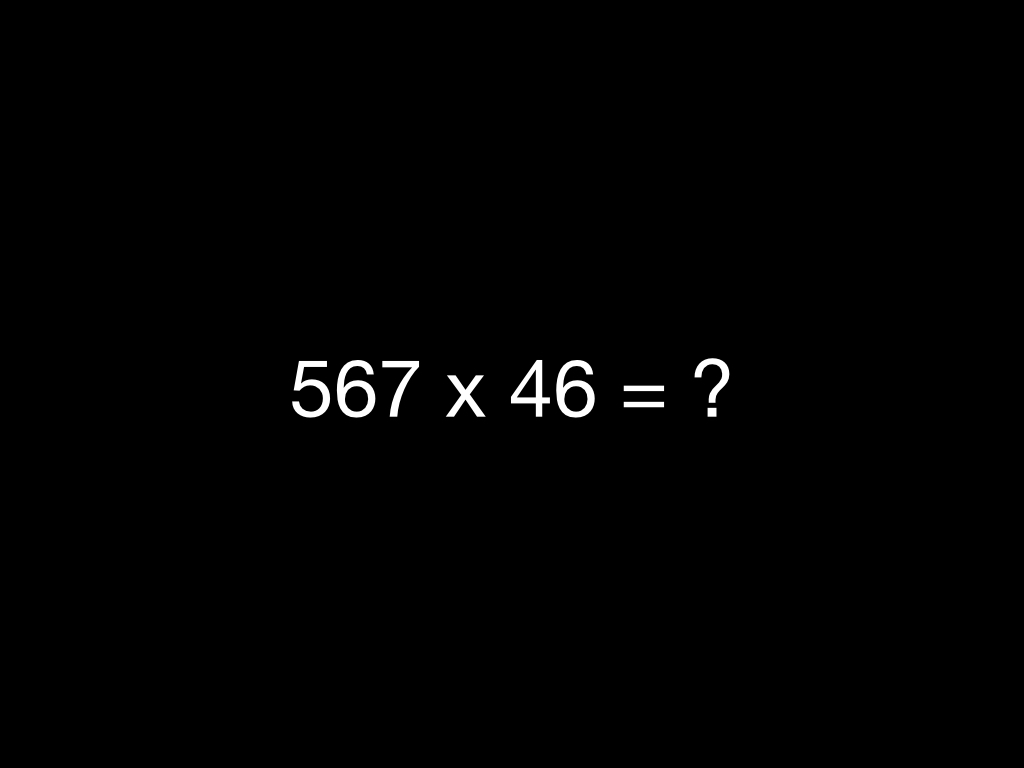
This is a routine problem for most adults because the know what to do and how to do it. Note that routine doesn’t mean easy.

In contrast, nonroutine problems are problems for which the learner does not immediately know a usable solution method. For example:



One approach to solving this is to reason that all 36 have at least two wheels for a total of 36 x 2 = 72 wheels. Since there are 80 wheels in all, the eight additional wheels (80-72) must belong to 8 tricycles, so there are 36-8 = 28 bikes.

Another approach would be to guess and check, yet another would be to form an algebraic representation and solve it that way.



An expert problem-solver could not only come up with several approaches to a problem like that, but could also flexibly choose among them to find the most suitable.

So how do they do that? Well, one thing we know, is that a key difference between an expert problem-solver and a novice problem-solver, lies in their ability to form a mental model of the problems essential components.



And researchers learned from observation that it’s this mental model that allows experts to be flexible.

Consider the following problem:



Researchers discovered that in a common superficial method used by poor problem-solvers, students focus on the numbers in the problem and use keywords to cue appropriate arithmetic operations. For example, the quantities $1.13 and 5 cents are followed by the keyword less, suggesting that the student should subtract 5 cents from $1.13 to get $1.08. Then the keywords how much and 5 gallons suggest that 5 should be multiplied by the result, yielding the incorrect answer of $5.40.

In contrast, a more proficient approach they witnessed was students constructing a problem model. A problem model is…any form of mental representation that maintains the structural relations among the variables in the problem. For example, a line graph with the gas stations on it.

To back up these findings, researchers studied students’ eye fixations and noticed that good problem-solvers were likely to focus on terms such as ARCO, Chevron, and this...



While less successful problem-solvers tended to focus on specific numbers and keywords…rather than the relationships among the quantities.



What’s happening here is that poor problem-solvers are looking at surface features of problems, where-as expert problem-solvers are focusing more on the structural relationships within the problems, relationships that provide the clues for how problems might be solved.

So this is literally what is happening inside the brain of a playtester spinning their wheels in your game.

They are using novice problem-solving skills, attempting to map a superficial solution onto your problem, and when it doesn’t work out, they don’t know what to do, assume that they must have operated the methodology wrong, and try again.



Now, as game designers, when we think about how we would solve the problem of a frustrated and stuck user, It’s unlikely that we would say: well, they’re just a bad problem-solver, and leave it at that. Instead, we’d probably try to build a tutorial to teach that user a series of skills to turn the non-routine problem they’re facing, into a routine one. But interestingly, this approach isn’t one of trying to improve their problem-solving skills, it’s one of trying to get around their problem-solving skills.

So where does this other approach come from?
Likely, it comes from another theory I want to talk about today: Constructivist theory.



This will be a shorter explanation.

Constructivist theory is based on the belief that learners learn by doing, as opposed to being told. One common way to teach constructively would be to instead of telling a student how a task works, give them a series of semi-routine problems to solve, leading them towards an answer. In this way, learners are still solving problems themselves, but they are doing so in a fairly linearly guided way that doesnt rely on them being expert-problem-solvers.



For example, one constructivist way to teach multiplication to someone who can count is to first help them learn how to skip count. (Skip counting for example is like if you want to skip count by 2, you'd sit a few learners in a circle and count around the circle, having the odd learners whisper their numbers, and the even ones speak loudly). Skip Counting is, a semi routine problem for somebody who already knows how to count. And then you could teach them how to multiply because multiplying is a semi-routine problem if you know how to skip count (you can see multiplying by 2 is very similar to skip counting by 2).

This methodology does a great job balancing focused direction with self-learning. It works great as long as you can tailor your lesson both to where learners are starting from and to how big a leap learners are comfortable taking from a routine problem to a semi-routine problem based off of how good their problem-solving skills are.



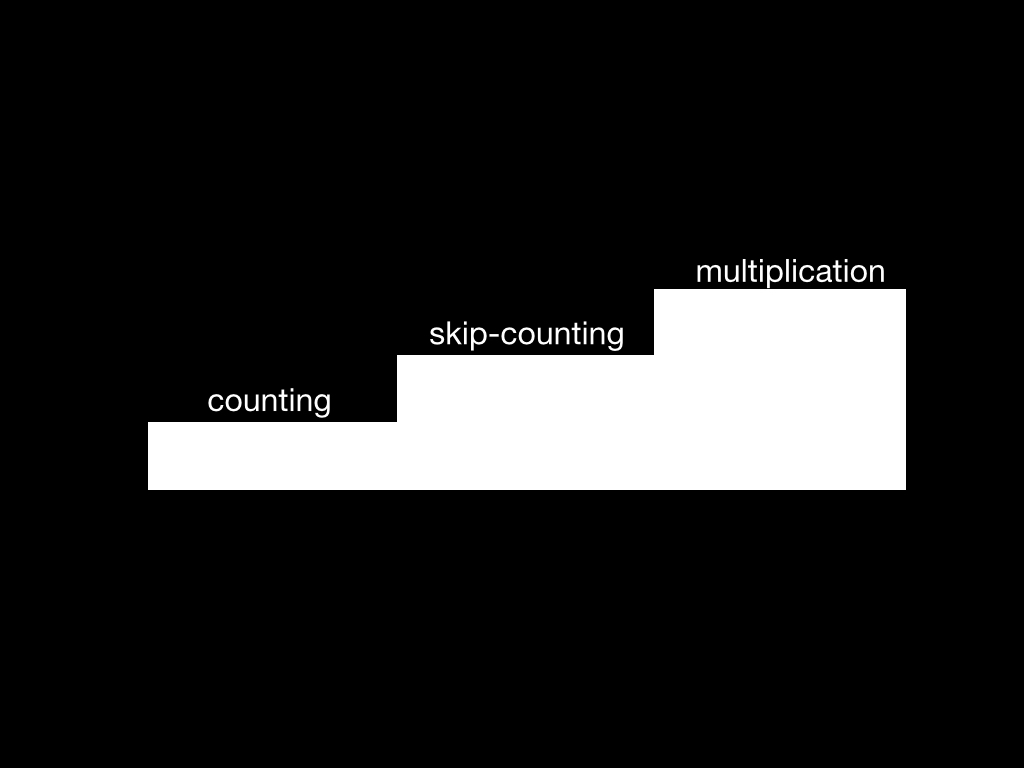
Constructivist theory lends itself well to this step-style of learning. Each new lesson is based off of your understanding of a previous lesson. Doesn't that sound an awful lot like tutorials in games?



So here’s where this gets interesting right? When we take these theories and look at games through them, we suddenly have language to talk about some complex aspects of difficulty. This is because games are primarily vehicles for problem-solving. In some games the problems are abstract spacial problems, in others they’re mathematical, combinatorial, verbal, or statistical.

When we think about the difficulty of games, we’re often referring to the difficulty of a particular problem or set of problems within a game. And we’re often thinking of difficulty in a step-wise mindset. We’re thinking of difficulty like simple algebra problems vs. hard algebra problems — stepwise difficulty, and how these steps relate specifically specifically to each other is how we tend to imagine the overall difficulty of our games.



What we’re often not thinking about, is the difficulty of understanding a new type of problem.



The difficulty of Non-Routine problems (hard) vs. Routine problems (easy). This is the type of difficulty that problem-solving gives us the language to think about. This is the language of accessibility-difficulty.



Because truly, difficulty is most often function of routine-ness.

Solving one multiplication problem is no easier than solving ten, but is easier than solving an algebra problem — until you understand algebra, then they’re basically the same difficulty. Complexity is only hard when it is foreign, when complexity is routine, it becomes work.

But we don’t think this way as developers.

Often, I hear difficulty explained as a muddled mixture of work-quantity and non-routine-ness, or as a performative measure (how fast can you do these 10 multiplication problems). But even there, speed is initially a function of how routine the problem is.

Interestingly there though, problem-solving is only relevant to speed up to a point — after that it’s primarily a function of how good you are at applying superficial methodologies or mechanical skill. Given our general avoidance of non-routine problems in games it’s not surprising how many of our games are speed oriented — how many of them base their difficulty around speedy execution of routine problems.



Anyway, There are a myriad of reasons why we don’t often think about the accessibility problems in games.

I believe primarily we don’t think about them because we aren’t often creating substantially new types of problems. Every bejewled-like is effectively a routine problem to anyone whose played any other bejewled-like, and because of that, similar solution methods can be employed in across the genre. A player doesn’t have to be a good problem-solver to approach a game that is similar to one they already understand. In other words, a player doesn’t need to be an expert problem-solver to approach and solve a routine problem, they can use novice superficial techniques.



Now when we think about hardcore and casual games through the step-difficulty mindset we would be tempted to classify hardcore games as hard, because often the problems usually involve steeper and longer flights of steps, and casual games as easy, because the problems in them usually consist of smoother, shorter flights — although its worth pointing out that this is not always the case, consider candy crush saga.

But interestingly, if we think of these two categories through the lens of problem-solving theory, we find that only the most ardent of gamers, that play games like spelunky, dark souls, dwarf fortress, and sunday crosswords, are truly embracing non-routine problems (problems that we could classify as hard). For everyone else, theres Plants Vs. Zombies 2, FIFA 14, Call of Duty 13, Angry Birds 5, and Assassins Creed 21 (if you count all the spinoffs).

So I think given this information, it’s important to think about hard difficulty not universally as a quality of hardcore games and easy difficulty not universally as a quality of casual games. I’ve found anecdotally that most people enjoy non-routine or semi-routine challenges as long as they find them accessible, and that really, the major difference between most casual and hardcore gamers is the set of problems that they find to be routine and have the superficial skills for.



Weirdly, I find we don’t often talk about accessibility through this lens when building tutorials for our games. So often we ignore whether or not our the player is a good or bad problem-solver, and instead assume a position of teaching the player our game through constructivist theory.

But games are not mathematics. They’re not a universal standardized framework, and they’re not taught to players by living people who can adjust their lessons to a particular learners ability. Because of this misalignment, we’re forced to design tutorials geared to the lowest reasonable skill set. But then we need to worry about being boring, so the cleverest constructivist tutorials have hidden goals, to keep experts from nodding off.

Consider Super Meat Boy, who’s worlds are filled with secrets and time-records to keep pros busy, while novices are given a slow build up to hone their skills. But even then, with it’s perfect constructivist tutorial, Super Meat Boy is still not a game made for everyone. It’s a game made for hardcore platform gamers. It’s a game that reasonably assumes a certain knowledge base of it’s constituents. And while these assumptions restrict the game to a niche, they’re also what make Super Meat Boy’s tutorial so successful. Which is great. So if you’re building a step-wise tutorial, understand that you are targeting a niche and revel in it.

Because this kind of constructivist framework leaves us in trouble if we want to consider how to introduce truly new players to our games. How does a casual game player ever get into Super Meat Boy? The problems we’d be leveling at that gamer are phenomenally non-routine.

There’s literally no semi-routine step for a player in that context. Following a step-wise tutorial that long and comprehensive would take years. Yet, instead of trying something else, many games simply stretch out their constructivist tutorials to attempt to account for more and more distant routine contexts, and simply throw up their hands up in the air when they fail.



This is why in Assassins Creed 2 there is literally an achievement for following another character through a linear set of hallways. This is attempting to teach you how to control your character with a joystick. This is ridiculous. This is like making a game about algebra and giving people an achievement for learning how to count. Nobody is ever going to close that kind of learning gap within a single game in this way. Instead of teaching new players how to tackle these truly and inescapably non-routine problems, we’re struggling against reality to cram enough steps in to turn them into semi-routine problems so we can teach the player using a methodology that no longer applies.



But fair enough right? Because how in the world would we actually accomplish such a complex educational task as helping a poor problem-solver to become an expert problem-solver? We just make games right?

And yet, there are a number of games out there that seem to appeal to everyone. Games that have set the world on fire and taught massively diverse players complex skills. Pac Man introduced the world to hardcore arcade games. Tetris introduced us to the joys of mobile gaming. Minecraft introduced us to 3d first person worlds and online multiplayer. And my own game, SpellTower, which is not in the same category as these other mega hits, has nonetheless introduced many technophobic grandmas to the joys of computer gaming.

How is this possible?



Well, it turns out there actually is one weird trick to enable non-expert problem-solvers to solve problems that are out of their league. It’s an incredibly powerful technique when you’re able to wield it because it allows you to make entirely new games appreciable to everyone, as well as build tutorials and difficulty curves, even in more typically routine games that are tuned across the board for expert and novice problem-solvers alike, without needing to fill your game with external rewards.



The trick is in the formulation of the problem-model. And this is actually how I came across this topic to begin with. As I randomly learned a few weeks ago, my mom’s phd thesis was one of the first papers to discover this technique back in the 80s. How weird, that the work she did and the work I do are so close and we never knew it. Anyway-



If you provide novice problem-solvers with a problem, they’ll attempt to solve it using superficial strategies, comparing it to routine problems that they already understand. This much I have covered already. But if you provide novice problem-solvers with — instead of a problem — a set of constraints, and then ask them to form and solve their own complex problems, something amazing happens — they solve these problems with expert-level strategies.

It’s the difference between teaching someone to fish, and having them invent things to do around a pond with a hook line and stick.



Personally, I suspect the reason this works has to do with the difficulties in constructing a problem model while under the stress of needing to solve it.

Remember, if we look back at the ARCO question, we find learners instead of building a model at all, focusing on the arithmetic keywords to solve the problem without understanding the problem, compared to expert problem-solvers who attempt to build a model first.

When you ask learners to provide their own problems, and constrain this request to problems to a certain difficulty, you’re forcing learners to internalize the constraints and focus first on building a problem model, before stressing them out with having them find a solution. Once they have this problem model in hand, they’re fully equipped with all the tools they need to behave as an expert problem-solver.

That’s a little bit abstract, so I’m going to walk you through how I employed this strategy intentionally in one of my games, and how i’ve seen it employed (possibly accidentally) elsewhere.



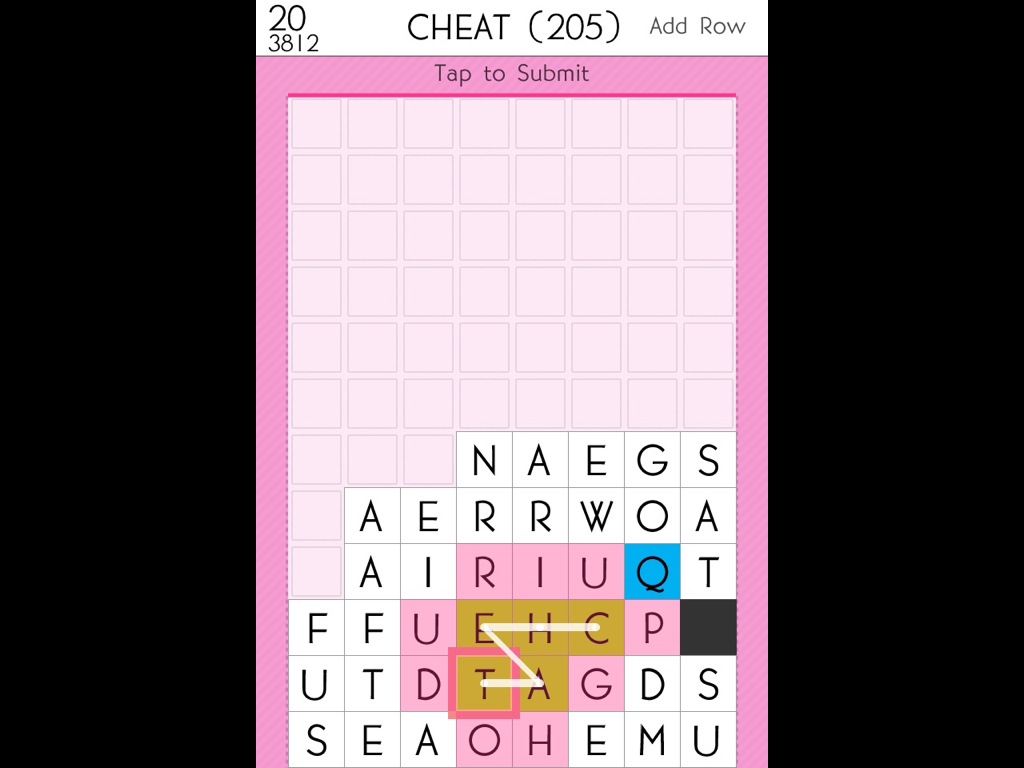
SpellTower, if you’re not familiar with it, is a game that sort of combines word-searches and Tetris. Every time you spell out a word, it’s letters are removed from the board, and a new row of letters is added to the bottom, and if any of the letters reach the top row, you lose.



The main secret to SpellTower’s success is that it’s is a game with two tutorials.

The first one is on the surface, and is actually more of an instruction manual than a tutorial. It’s all about presenting the constraints of the system to the player.

The second tutorial is hidden. It masquerades as a game mode called Tower Mode.



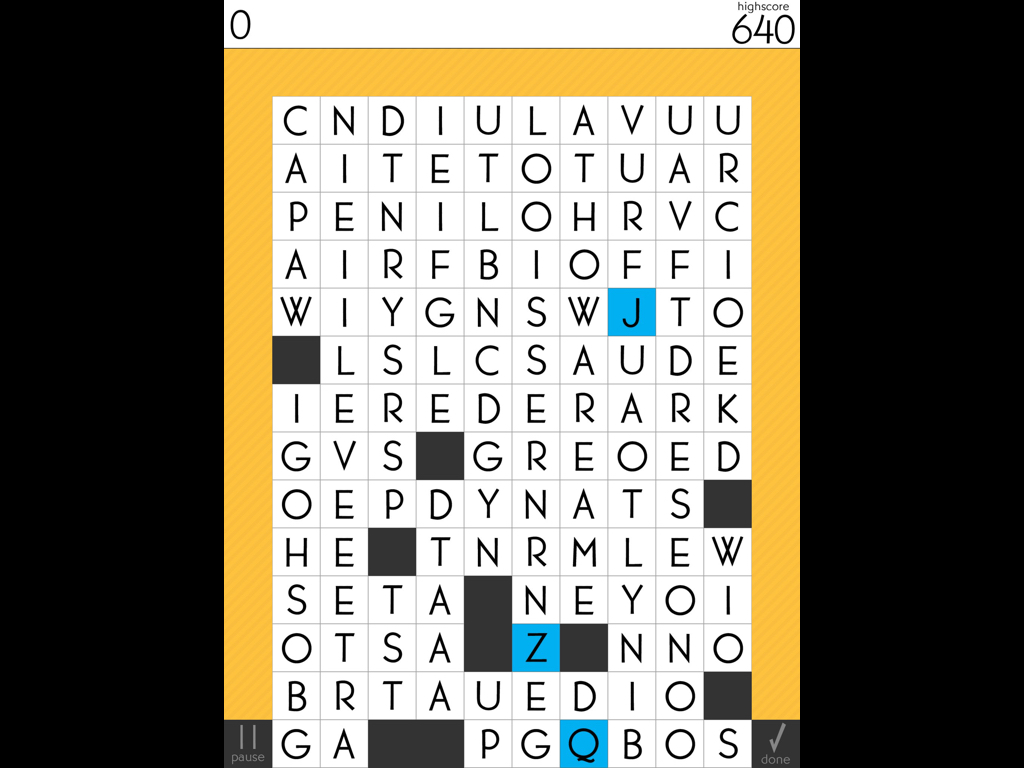
Unlike the other 3 modes in SpellTower, Tower Mode, has no explicit goals, no pressure (neither time nor systemic), no additional letters beyond what you start with, and no end condition. Tower Mode ends when you say you’re done. Most often players say they’re done when the letters run out.



What’s fascinating about watching players play tower mode, is that absent of any problems to be solved, players are forced to invent their own problems. Problems like “Can I spell a 6 letter word?” or “Can I spell a word with a Q in it?” or “What’s the highest score I can get from a single word?” or “what’s the highest score I can get over-all?” or “Can I manage to clear out all of the letters from the screen, with none remaining?” or “Can I re-arrange the letters through finding and eliminating words to spell out a particular word?”

There are two important qualities that all of these questions share. The first is that none of them are particularly better or more fun than the rest. Some are harder than others, in a step-wise sense, but they’re all worthwhile and challenging goals.

The second is that answering any of these questions will teach you things that make you better at SpellTower. These questions aren’t just idle exploration into the corners of a system, they’re a self-guided tour into the exact areas of the system that matter.

Just as a side note here, it’s interesting to me how this is the inverse of what we typically do with achievements, where if we do reward exploration, it’s usually only exploration into fun but ultimately irrelevant corners of the system. I’m guilty of this too in my game Bit Pilot.



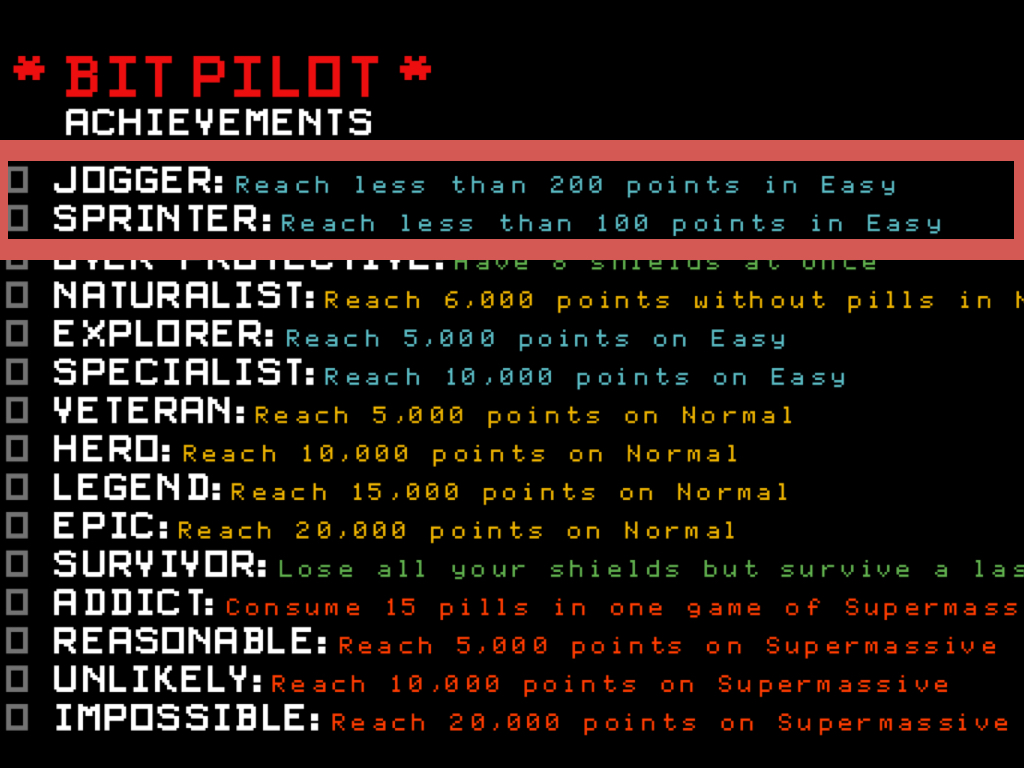
(These are two Bit Pilot achievements that reward you for losing quickly, something that’s actually pretty tough and interesting, and yet, learning how to lose is clearly something that won't teach you better strategies in the normal game.)



But anyway, back to SpellTower, so essentially what we have here is literally a constraint based system that asks players to find and create their own complex non-routine problems and then solve them. And the result is players of all types applying expert level problem-solving skills to learn how to play and enjoy SpellTower. After comfortably exiting this mode players of all kinds have learned, on their own, expert play strategies, all without loading-screen hints or explicit tutorialization. Additionally, while i require that players play tower mode before playing anything else, because they can simply end the mode whenever they want, if expert problem-solvers end up feeling bored, they can simply move on to the main game.

I believe this mode primarily has allowed SpellTower to be exciting for kids to adults to grandparents, casual and hardcore gamers alike.



It’s this quality of constrained sandboxes contained inside standard goal oriented gameplay that we see over and over again in the many of the most successful accessible games.

Some of them, like Minecraft literally retain these sandbox characteristics the entire time, and includes a creative mode in which there are no challenges.

Others are less explicitly sandboxes, but still manage to have many support sandbox style exploration.

Pac Man manages to support this kind of play through obfuscation of its goals (pacman never tells you how to get to the next level, or even if there is a next level), and clearly defined components. This provides opportunity to for players to create their own goals, many of which are more exciting to novices than actually trying to achieve a highscore.

Goals like:
- collecting all the dots
- eating a giant blinking dot
- eating all the giant blinking dots
- eating all the ghosts after eating a giant blinking dot
- surving as long as possible
- eating the fruit

Again, the key with these goals is that they’re all in service of improving your pacman skills.

In Tetris, the slow initial speed and pure sandbox novelty of coming up with interesting shape combinations, or trying to get 2, 3 or 4 rows at a time can be enough to keep people going long before they start attempting highscores.

Now, I’m not saying all games have to be taught this way, but I do think it’s worth having this in our toolbox. Because although each of these games seems like a straightforward videogame, we can use the lens of problem-solving to reveal one possible reason why they’re so accessible, and possibly, why they’re so popular.



And the most wonderful part of approaching players this way is that they don’t just act like great problem-solvers, they eventually become great problem-solvers. And having great problem-solvers playing your game is every designers dream, because these are the type of players who surprise you. They’re the type that master your game to a greater degree than you could have ever imagined. They’re the type that invent problems that are much more interesting then the ones you came up with for them. They’re the players who figure out how to beat Ocarina of Time in under 20 minutes, or start a league of Binding of Isaac Racing, or figure out how to play a single game of SpellTower for 6 months and amass a score of 2 million points.

Games are just rules until they are played, so it follows that a beautiful game is one that is played beautifully.



Lets design to help our players do that.